证明圆内接四边形的面积公式.
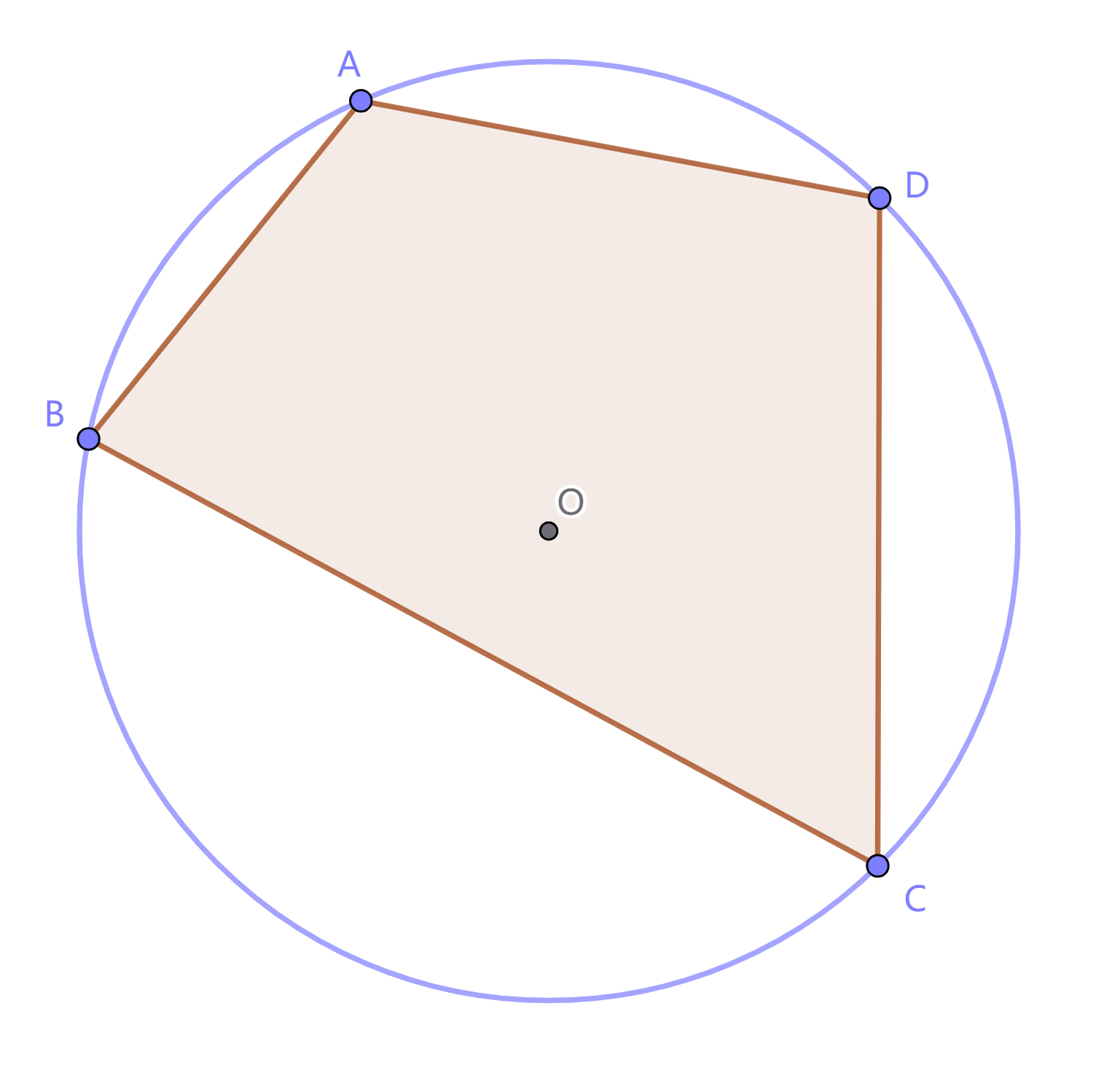
设 $ABCD$ 是圆 $O$ 的内接四边形, 四条边的长度分别为 $|AB|=a$, $|BC|=b$, $|CD|=c$, $|DA|=d$. 若 $p$ 是其周长的一半, 即 $p=\frac{1}{2}(a+b+c+d)$, 则 $ABCD$ 的面积为
\[
S=\sqrt{(p-a)(p-b)(p-c)(p-d)}.
\]
首页
欢迎
Welcome
欢迎, 这是一个学习数学、讨论数学的网站.
转到问题
请输入问题号, 例如: 2512
|
IMAGINE, THINK, and DO How to be a scientist, mathematician and an engineer, all in one? --- S. Muthu Muthukrishnan |
Local Notes
Local Notes 是一款 Windows 下的笔记系统.
Sowya
Sowya 是一款运行于 Windows 下的计算软件.
详情
下载 Sowya.7z (包含最新版的 Sowya.exe and SowyaApp.exe)
注: 自 v0.550 开始, Calculator 更名为 Sowya. [Sowya] 是吴语中数学的发音, 可在 cn.bing.com/translator 中输入 Sowya, 听其英语发音或法语发音.
注册
欢迎注册, 您的参与将会促进数学交流. 注册
在注册之前, 或许您想先试用一下. 测试帐号: usertest 密码: usertest. 请不要更改密码.